Simple Gearbox Tutorial

1 - Introduction

The objective of this tutorial is to understand how to optimize the fuel consumption of a car which goes through a WLTP cycle by finding the best gear ratio configuration for its gearbox. So in order to do this there are some specifications that must be considered, such as the following ones:

Gear ratios must vary only inside an imposed range;
Gear selection must satisfy imposed speed ranges;

2 - Build the bot in 5 steps

Before beginning, you have access to the tutorial9 file in the tutorials folder cloned as explained in the first tutorial. We will apply the DessIA method to find the best solution to our problem.

2.0 - Formatting model engineering data

Before we dive right into the engineering system steps, this first step is very important to mention because it will format most part of the data needed for the following calculations.

For this first step, we have created two classes, the EfficiencyMap and WLTPCycle. The first one is responsible for calculating the Break Specific Fuel Consumption (BSFC) as well as the Efficiency values for the engine, this will help us later determine the fuel efficiency at each given configuration. To do so, the class is initialized with some engine parameters such as a list of engine speeds and another one of engine torques, a matrix of fuel mass flow rate in which each value corresponds to one configuration of the engine's speed and torque, in addition to the lower heating value of the fuel used followed by a name. The BSFC and efficiency were calculated using the respective following formulas:

Break Specific Fuel Consumption:

${\normalsize{BSFC = \frac{\normalsize 1} {\normalsize {\mathbf{\omega}} \cdot \normalsize \tau}}}$

Efficiency:

${\normalsize{\mathbf{\eta} = \frac{\normalsize 1} {\normalsize BSFC \cdot \normalsize Q \text{\textunderscore} hv}}}$

class EfficiencyMap(DessiaObject):
    _standalone_in_db = False
 
    """
    Build the engine map and then determine its efficiency
    """
    def __init__(self, engine_speeds: List[float], engine_torques: List[float], mass_flow_rate: List[Tuple[float, float]],
                 fuel_hv: float, name: str = ''):
        self.engine_speeds = engine_speeds                                      # in rad/s
        self.engine_torques = engine_torques                                    #in Nm
        self.mass_flow_rate = mass_flow_rate
        self.fuel_hv = fuel_hv                                                  #fuel lower heating value in J/kg
 
        DessiaObject.__init__(self,name=name)
 
        BSFC = []
        for i, engine_speed in enumerate(self.engine_speeds):
            list_bsfc = []
            for j, engine_torque in enumerate(self.engine_torques):
                bsfc = self.mass_flow_rate[i][j]/(engine_speed*engine_torque)   # in kg/J
                list_bsfc.append(bsfc)
            BSFC.append(list_bsfc)
        self.bsfc = BSFC
 
        efficiencies=[]
        for list_bsfc in BSFC:
            list_efficiencies=[]
            for bsfc in list_bsfc:
                efficiency = 1/(bsfc*self.fuel_hv)
                list_efficiencies.append(efficiency)
            efficiencies.append(list_efficiencies)
        self.efficiencies = efficiencies

The second one, WLTPCycle is responsible for finishing the calculations for the cycle torques in the wheel of the car, and for that it receives as parameters the cycle speeds, the mass of the car, the tyre radius and the time interval between each cycle point, and as always, a name. In the image shown below we can see how the torque in the wheel is calculated, first we find the car acceleration between each two velocity points and then with the car mass and the tyre radius, we can then find the torque.

class WLTPCycle(DessiaObject):
    _standalone_in_db = False
    """
    WLTP cycle paremeters and wheel torque calculations
    """
    def __init__(self, cycle_speeds: List[float], car_mass: float, tire_radius: float, dt: float = 1, name: str = ''):
        self.cycle_speeds = cycle_speeds
        self.car_mass = car_mass
        self.tire_radius = tire_radius
        self.dt = dt
        DessiaObject.__init__(self,name=name)
 
        accelerations = []
        for i in range(len(self.cycle_speeds[:-1])):
            acceleration = (self.cycle_speeds[i + 1] - self.cycle_speeds[i]) / dt   # acceleration in m/s^2
            if acceleration < 0:
                acceleration *= -1
            accelerations.append(acceleration)
 
        cycle_torques=[]
        for acceleration in accelerations:
            torque = acceleration*car_mass*tire_radius/2                            #torque in Nm
            cycle_torques.append(torque)
 
        self.cycle_torques = cycle_torques

2.1 - Describe your engineering system

Our engineering system is basically composed of two components, an engine and a gearbox. So as you have seen in previous tutorials, there is a class dedicated for each one of these components.

The Engine class is initialized following 3 main requirements, it receives an EfficiencyMap object with all the important information concerning its efficiency parameters along with a speed and torque set point parameters for the engine's idling state. These last two parameters mentioned will be important while determining gears when the car is actually stopped.

class Engine(DessiaObject):
    _standalone_in_db = True
 
    def __init__(self, efficiency_map: EfficiencyMap, setpoint_speed: float, setpoint_torque: float, name:str=''):
        self.efficiency_map = efficiency_map
        self.setpoint_speed = setpoint_speed
        self.setpoint_torque = setpoint_torque
 
        DessiaObject.__init__(self,name=name)

The GearBox class receives as inputs at least two parameters, an engine object and a list of speed ranges where each given range corresponds to one gear configuration, that is the first range stands for the first gear, and the last one for the last gear. It is important to note that one range can intersect with the next one.

class GearBox(DessiaObject):
    _standalone_in_db = True
 
    def __init__(self, engine: Engine, speed_ranges: List[Tuple[float, float]] = None, ratios: List[float] = None, name: str = ''):
        self.engine = engine
        self.speed_ranges = speed_ranges
        self.ratios = ratios
 
        DessiaObject.__init__(self,name=name)

2.2 - Define engineering simulations needed

Two methods were created in the Engine class, efficiency and consumption_efficiency. These two methods receive two engine parameters: a speed and a torque. Using these entry parameters and the 2D interpolation method from scipy, they calculate the engine efficiency or the engine fuel efficiency from the EfficiencyMap object and the corresponding value is returned from the respective method. These methods will be important later when optimizing our gearbox.

class Engine(DessiaObject):
    _standalone_in_db = True
 
    def __init__(self, efficiency_map: EfficiencyMap, setpoint_speed: float, setpoint_torque: float, name:str=''):
        self.efficiency_map = efficiency_map
        self.setpoint_speed = setpoint_speed
        self.setpoint_torque = setpoint_torque
 
        DessiaObject.__init__(self,name=name)
 
    def efficiency(self, speed:float, torque:float):
        interpolate = interp2d(self.efficiency_map.engine_torques, self.efficiency_map.engine_speeds, self.efficiency_map.efficiencies)
        interpolate_efficiency = interpolate(torque, speed)
        return interpolate_efficiency[0]
 
    def consumption_efficiency(self, speed:float, torque: float):
        interpolate = interp2d(self.efficiency_map.engine_torques, self.efficiency_map.engine_speeds, self.efficiency_map.bsfc)
        interpolate_consumption_efficiency = interpolate(torque, speed)
        return float(interpolate_consumption_efficiency[0])

2.3 - Create an Optimizer

The next step is to create an optimizer to our tutorial. If you have gone through all the previous tutorials you have realized that we use the minimize method from scipy.optimize quite often and here we will use it once again. To do so, a class called Optimizer is first created, where all methods needed to achieve the final purpose are created. The class optimizer is initialized with a few parameters such as a gearbox and a WLTP Cycle object which were created just above, along with a first_gear_ratio_min_max parameter which stands for the range of possible ratio values for the first gear. The last entry parameter needed is a list of coefficient ranges used to determine the relation between the actual gear and the previous one. The coeff_between_gear is primarily set as None, but if specified differently it should have (number of gears - 1) coefficient ranges.

class GearBoxOptimizer(DessiaObject):
    _standalone_in_db = True
 
    def __init__(self, gearbox: GearBox, wltp_cycle: WLTPCycle, firstgear_ratio_min_max: Tuple[float,float], coeff_between_gears: List[Tuple[float, float]] = None, name: str = ''):
        self.gearbox = gearbox
        self.wltp_cycle = wltp_cycle
        self.coeff_between_gears = coeff_between_gears
        self.firstgear_ratio_min_max = firstgear_ratio_min_max
        DessiaObject.__init__(self,name=name)

2.3.1 - Defining the x vector

The minimize method used needs a x vector that specifies the parameters to be optimized. For this particular tutorial the x vector is composed of the first element being the ratio of the first gear of the gearbox and the following ones being the coefficients between each two gears. The number of parameters in the x vector is as big as the number of gears of our gearbox.

2.3.2 - Defining Bounds for Optimization

For each one of the parameters in the x vector, we must define a bound, that is, a minimum and maximum value possible fo this parameter. For our first bound corresponding to the first gear ratio, we use the first_gear_ratio_min_max parameter given by the user, and the for the bounds of coefficients between each two gears, we use the coefficient range of the coeff_between_gears parameter. This last parameter if not specified by the user, all ranges are set with the same pre defined value.

class GearBoxOptimizer(DessiaObject):
    _standalone_in_db = True
 
    def __init__(self, gearbox: GearBox, wltp_cycle: WLTPCycle, first_gear_ratio_min_max: Tuple[float,float], coeff_between_gears: List[Tuple[float, float]] = None, name: str = ''):
        self.gearbox = gearbox
        self.wltp_cycle = wltp_cycle
        self.coeff_between_gears = coeff_between_gears
        self.first_gear_ratio_min_max = first_gear_ratio_min_max
        DessiaObject.__init__(self,name=name)
 
        if self.coeff_between_gears == None:
            self.coeff_between_gears = (len(self.gearbox.speed_ranges)-1)*[[0.5,1]]
 
        bounds=[]
        for i in range(len(self.gearbox.speed_ranges)):
            if i == 0:
                bounds.append([self.first_gear_ratio_min_max[0],self.first_gear_ratio_min_max[1]])
            else:
                bounds.append([self.coeff_between_gears[i-1][0], self.coeff_between_gears[i-1][1]])
        self.bounds = bounds

2.3.3 - Initial Conditions

The initial condition for this tutorial is created using exactly the same reasoning as you have seen in the tutorial 2 and 3.

def cond_init(self):
        x0 = []
        for interval in self.bounds:
                x0.append((interval[1]-interval[0])*float(np.random.random(1))+interval[0])
        return x0

2.3.4 Create an update method

Before we build the objective function it is important to create an update method which receives the vector x and with it, updates the ratios of the gearbox. These parameters will change during the optimization. When a method from the GearBox class is called, you have to make sure your object is up-to-date, ie. is updated with the newest x vector. This method is also used to verify all gear changes as well as other important parameters such as the fuel consumption and engine speeds which are stored in self parameters and some are used in the objective function later.

Methods in the Class GearBox

Update Method

To update the ratios an updated method is also created in the GearBox class, which also receives the vector x and what is does is that it takes the first ratio and with all the coefficients it updates all the gearbox ratios.

def update(self, x):
        ratios = []
        for i in range(len(x)):
            if i == 0:
                ratio = float(x[0])
                ratios.append(ratio)
            else:
                ratio *= float(x[i])
                ratios.append(ratio)
        self.ratios = ratios

Gear_choice Method

The second method created in GearBox is "gearchoice", which receives two parameters: the wltp speed and torque at a time **_t** of the cycle. This method choses the gears that the gearbox is supposed to be by using the speed_ranges parameter from the GearBox object, and with this information it then calculates the engine speed and torque using the corresponding ratio which are used to find the fuel consumption at this configuration using the "consumptionefficiency" method from the Engine class presented above. Because the ranges from the _speed_ranges parameter may intersect one another, all possible configurations are saved in lists and at the end, the configuration that gives the lowest consumption efficiency is chosen. This method returns the gear choice along with other important parameters for the final result's post-treatment analyses.

def gear_choice(self, cycle_speed, cycle_torque):
        fuel_consumption_gpkwh = 0
        engine_speed = 0
        engine_torque = 0
        gear = 0
        ratio = 0
 
        if cycle_speed == 0:
            engine_speed = self.engine.setpoint_speed
            engine_torque = self.engine.setpoint_torque
            fuel_consumption_gpkwh = self.engine.consumption_efficiency(engine_speed, engine_torque)
            gear = 0
            ratio = 0
        else:
            list_ratio = []
            list_gear = []
            list_fuel_c = []
            list_torque = []
            list_speed = []
            for i, speed_range in enumerate(self.speed_ranges):
                if cycle_speed  >= speed_range[0] and cycle_speed  < speed_range[1]:
                    ratio = self.ratios[i]
                    engine_speed = cycle_speed * ratio
                    engine_torque = cycle_torque / ratio
                    fuel_consumption_gpkwh = self.engine.consumption_efficiency(engine_speed, engine_torque)
                    gear = i + 1
                    list_ratio.append(ratio)
                    list_gear.append(gear)
                    list_fuel_c.append(fuel_consumption_gpkwh)
                    list_speed.append(engine_speed)
                    list_torque.append(engine_torque)
 
            fuel_consumption_gpkwh = min(list_fuel_c)
            ratio = list_ratio[list_fuel_c.index(fuel_consumption_gpkwh)]
            gear = list_gear[list_fuel_c.index(fuel_consumption_gpkwh)]
            engine_speed = list_speed[list_fuel_c.index(fuel_consumption_gpkwh)]
            engine_torque = list_torque[list_fuel_c.index(fuel_consumption_gpkwh)]
 
        return [ gear, ratio, fuel_consumption_gpkwh, engine_speed, engine_torque]

So finally the update method from the Optimizer class is shown is the scheme below.

 def update(self, x):
        self.gearbox.update(x)
 
        fuel_consumptions = []
        gears = []
        ratios = []
        engine_speeds = []
        engine_torques = []
 
        for (cycle_speed, cycle_torque) in zip(self.wltp_cycle.cycle_speeds, self.wltp_cycle.cycle_torques):
            cycle_speed = cycle_speed*2/self.wltp_cycle.tire_radius
            gear_choice = self.gearbox.gear_choice(cycle_speed, cycle_torque)
            gears.append(gear_choice[0])
            ratios.append(gear_choice[1])
            fuel_consumptions.append(gear_choice[2])
            engine_speeds.append(gear_choice[3])
            engine_torques.append(gear_choice[4])
 
 
        self.engine_speeds = engine_speeds
        self.engine_torques = engine_torques
        self.gears = gears
        self.ratios = ratios
        self.fuel_consumptions = fuel_consumptions

2.3.5 - Create an objective function

To build the objective function it is important to remember what it is that is being optimized and in this tutorial we aim to minimize the car fuel consumption through a wltp cycle by optimizing the gearbox ratios. Therefore the objective function takes into account the average fuel consumption of the cycle calculated with the gear ratios updated with the vector x as explained above. In addition, a condition was created to check if the engine torque exceeds the maximum torque permitted. If this happens, a big positive number is added to the objective function, which will allow the elimination of this solution during the validation step.

def objective(self, x):
        self.update(x)
        objective_function = 0
 
        objective_function += mean(self.fuel_consumptions)
 
        for engine_torque in self.engine_torques:
            if engine_torque > max(self.gearbox.engine.efficiency_map.engine_torques):
                objective_function += 1000
 
        return objective_function

2.3.6 - Create an optimize method

The next step is to finally build an optimize method inside the class Optimizer which calls the minimize method from scipy inside a while loop so it can try to minimize the objective function several times and at each time use a different initial condition that may help find better solutions. To validate a solution, two dontitions are used: it is verified that there was no issue during the minimization process with .success method and it is also verified that the maximum torque is valid by comparing the minimize result value, which is actually the cycle's average fuel consumption, with the maximum fuel consumption value available in the consumption_efficiency parameter from the EfficiencyMap object. If the solution is validated, the current gearbox along with all important parameters needed for post-treatment analyses are saved into another object called GearBoxResults which will be explained later. This method returns all validated solutions.

def optimize(self, max_loops:int = 1000):
        valid = True
        count = 0
        list_gearbox_results = []
 
        while valid and count < max_loops:
            x0 = self.cond_init()
            self.update(x0)
            sol = minimize(self.objective, x0, bounds = self.bounds)
            count += 1
            if sol.fun < max([j for i in self.gearbox.engine.efficiency_map.bsfc for j in i]) and sol.success:
                self.average_fuel_consumption = float(sol.fun)
                self.update(list(sol.x))
                gearbox = self.gearbox.copy()
                gearbox.ratios = self.gearbox.ratios
                gearbox_results = GearBoxResults(gearbox, self.wltp_cycle, self.engine_speeds,  self.engine_torques,  self.fuel_consumptions,  self.gears, self.ratios, self.average_fuel_consumption)
                list_gearbox_results.append(gearbox_results)
 
        return list_gearbox_results

2.3.7 - Create a Class GearBoxResults to store the results of each solution

The objective of creating the GearBoxResults class is to have all the result parameters in one place and some of them are not necessarily an object's parameter, like for example the engine's speeds over the wltp cycle. Furthermore, a plot_data method is built to make it easier to visualize some particular parameters of each different solution.

class GearBoxResults(DessiaObject):
    _standalone_in_db = True
 
    def __init__(self, gearbox: GearBox, wltp_cycle: WLTPCycle, engine_speeds: List[float], engine_torques: List[float], fuel_consumptions:List[float],
                 gears: List[float], ratios:List[float], average_fuel_consumption:float, name: str = ''):
        self.gearbox = gearbox
        self.wltp_cycle = wltp_cycle
        self.engine_speeds =engine_speeds
        self.engine_torques = engine_torques
        self.fuel_consumptions = fuel_consumptions
        self.gears = gears
        self.ratios = ratios
        self.average_fuel_consumption = average_fuel_consumption
        DessiaObject.__init__(self,name=name)
 
        self.average_engine_speed = mean(self.engine_speeds)
        self.average_engine_torque = mean(self.engine_torques)
        self.ratio_min = min(self.gearbox.ratios)
        self.ratio_max = max(self.gearbox.ratios)
        self.average_ratio = mean(self.gearbox.ratios)
 
 
    def plot_data(self):
 
        cycle_time = [i+1 for i in range(len(self.wltp_cycle.cycle_speeds[:-1]))]
        points=[]
        for car_speed, wheel_torque, engine_speed, engine_torque, fuel_consumption, time, gear in zip(self.wltp_cycle.cycle_speeds[:-1], self.wltp_cycle.cycle_torques ,self.engine_speeds,self.engine_torques, self.fuel_consumptions, cycle_time, self.gears):
            points.append({'c_s': car_speed,'whl_t': wheel_torque,'w_e': engine_speed,'t_e': engine_torque, 'f_cons (g/kWh)':fuel_consumption*3.6e9, 'time': time, 'gear': gear})
 
        color_fill = LIGHTBLUE
        color_stroke = GREY
        point_style = plot_data.PointStyle(color_fill=color_fill, color_stroke=color_stroke)
        axis = plot_data.Axis()
        """"""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""
        to_disp_attribute_names = ['c_s', 'f_cons (g/kWh)']
        tooltip = plot_data.Tooltip(to_disp_attribute_names=to_disp_attribute_names,)
        objects = [plot_data.Scatter(tooltip=tooltip, to_disp_attribute_names=to_disp_attribute_names,
                                     point_style=point_style,
                                     elements=points, axis=axis)]
        """"""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""
        to_disp_attribute_names = ['whl_t', 'f_cons (g/kWh)']
        tooltip = plot_data.Tooltip(to_disp_attribute_names=to_disp_attribute_names)
        objects.append(plot_data.Scatter(tooltip=tooltip, to_disp_attribute_names=to_disp_attribute_names,
                                      point_style=point_style,
                                      elements=points, axis=axis))
        """"""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""
        edge_style = plot_data.EdgeStyle()
        rgbs = [[192, 11, 11], [14, 192, 11], [11, 11, 192]]
        objects.append(plot_data.ParallelPlot(elements=points, edge_style=edge_style,
                                              disposition='vertical',to_disp_attribute_names = ['w_e','t_e','f_cons (g/kWh)'],
                                              rgbs=rgbs))
 
        coords = [(0, 0), (500, 0),(1000,0)]
        sizes = [plot_data.Window(width = 500, height = 500),
                 plot_data.Window(width = 500, height = 500),
                 plot_data.Window(width = 500, height = 500)]
        multiplot = plot_data.MultiplePlots(elements=points, plots=objects,
                                       sizes=sizes, coords=coords)
 
        list_colors = [BLUE, BROWN, GREEN, BLACK]
        graphs2d = []
        point_style = plot_data.PointStyle(color_fill=RED, color_stroke=BLACK, size = 1)
 
        """"""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""
        tooltip = plot_data.Tooltip(to_disp_attribute_names=['sec', 'gear'])
        edge_style = plot_data.EdgeStyle(line_width=0.5 ,color_stroke = list_colors[0])
        elements = []
        for i, gear in enumerate(self.gears):
            elements.append({'sec': cycle_time[i], 'gear': gear})
        dataset = plot_data.Dataset(elements = elements, edge_style = edge_style, tooltip = tooltip, point_style = point_style)
        graphs2d.append(plot_data.Graph2D(graphs = [dataset], to_disp_attribute_names = ['sec', 'gear']))
 
        """"""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""
 
        tooltip = plot_data.Tooltip(to_disp_attribute_names=['sec', 'f_cons (g/kWh)'])
        edge_style = plot_data.EdgeStyle(line_width=0.5 ,color_stroke = list_colors[0])
        elements = []
        for i, gear in enumerate(self.gears):
            elements.append({'sec': cycle_time[i], 'f_cons (g/kWh)': self.fuel_consumptions[i]*3.6e9})
        dataset = plot_data.Dataset(elements = elements, edge_style = edge_style, tooltip = tooltip, point_style = point_style)
        graphs2d.append(plot_data.Graph2D(graphs = [dataset], to_disp_attribute_names = ['sec', 'f_cons (g/kWh)']))
 
        """"""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""
 
        tooltip  = plot_data.Tooltip(to_disp_attribute_names=['sec', 'w_e'])
        edge_style = plot_data.EdgeStyle(line_width=0.5 ,color_stroke = list_colors[2])
        elements = []
        for i, torque in enumerate(self.wltp_cycle.cycle_torques):
            elements.append({'sec':cycle_time[i], 'w_e':self.engine_speeds[i]})
        dataset = plot_data.Dataset(elements = elements, edge_style = edge_style, tooltip = tooltip, point_style = point_style)
        graphs2d.append(plot_data.Graph2D(graphs = [dataset], to_disp_attribute_names = ['sec', 'w_e']))
 
        """"""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""
 
        tooltip  = plot_data.Tooltip(to_disp_attribute_names=['sec', 'w_t'])
        edge_style = plot_data.EdgeStyle(line_width=0.5 ,color_stroke = list_colors[3])
        elements = []
        for i, torque in enumerate(self.wltp_cycle.cycle_torques):
            elements.append({'sec':cycle_time[i], 'w_t':self.engine_torques[i]})
        dataset = plot_data.Dataset(elements = elements, edge_style = edge_style, tooltip = tooltip, point_style = point_style)
        graphs2d.append(plot_data.Graph2D(graphs = [dataset], to_disp_attribute_names = ['sec', 'w_t']))
 
        coords = [(0, 0), (0,187.5), (0,375), (0,562.5)]
        sizes = [plot_data.Window(width=1500, height=187.5),
                 plot_data.Window(width=1500, height=187.5),
                 plot_data.Window(width=1500, height=187.5),
                 plot_data.Window(width=1500, height=187.5)]
        multiplot2 = plot_data.MultiplePlots(elements=points, plots=graphs2d,
                                       sizes=sizes, coords=coords)
 
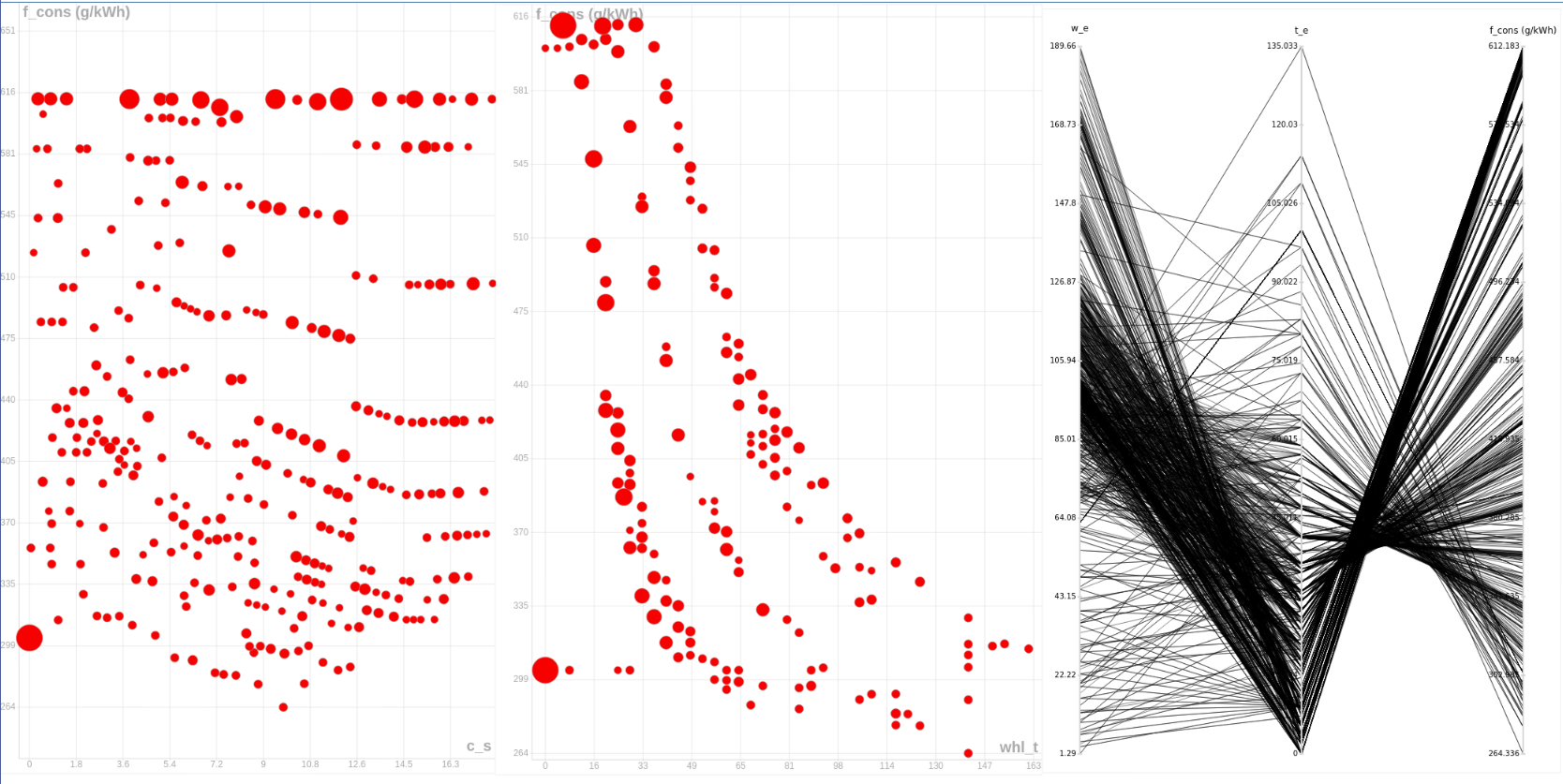
        return [multiplot, multiplot2]

For that, two multiplot types of data_plot were built. For the first Multiplot, two scatter plots were created, showing the fuel consumption as well as the relation between the car speed the fuel consumption and the wheel torque. In this first multiplot there is also a parallel plot showing the relation between the engine torque and speed and the fuel consumption. The results are shown in the first image below;

multiplot1

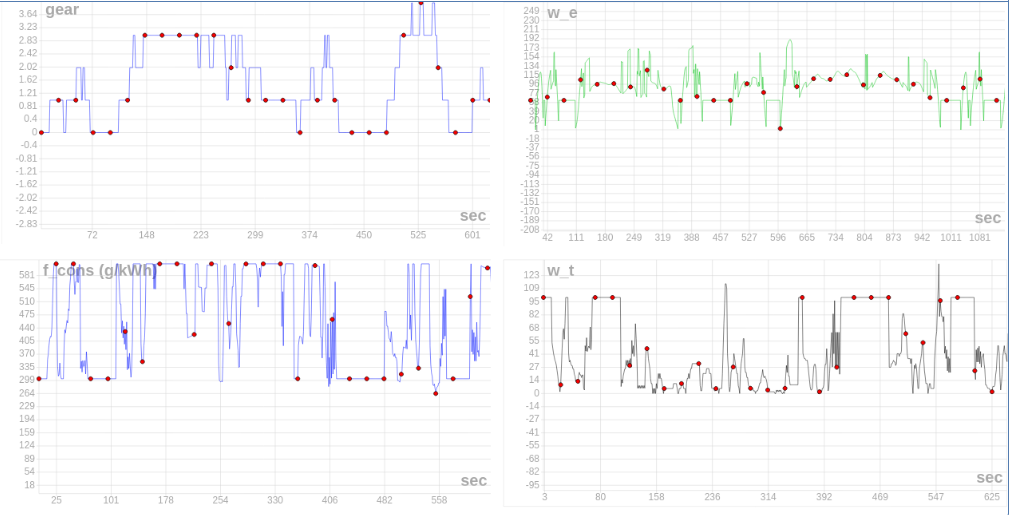
The second Multiplot created is actually a set of four 2D type graphs of different parameters over the time of whole WLTP Cycle. The first shows the different changes in gear over time. The second, the third and fourth respectively show the consumption, the engine speed and the torque speed over time, to allow us to have a view of what is happening during all cycle.

multiplot2

Script

As you might have seen before, to test our tutorial a script file is created. The script starts by defining the EfficiencyMap object and for that it uses some engine information such as a list of the engine's speed and torque and a fuel mass flow rate matrix where each value corresponds to one combination of engine speed and torque values, and the last parameter specified is the fuel lower heating value. When defining any object be sure that all specific parameters are well introduced in the SI units.

The next object to be defined is one from the WLTPCycle class, and for that we specify the list of the wltp cycle speeds as well as the mass and tire radius of the car plus the cycle time interval between one point and the next. Finally, with these first two objects created it is now possible to create the elements composing the engineering system. Now, to define the engine you only have to define the engine speed and torque setpoint, corresponding to the engine's goal state when it is stopped. The gearbox is then defined with the engine just created, alongside with the car speed ranges allowed by the gears. The last object defined is the GearboxOptimizer which is also initialized with the GearBox and WLTPCycle defined above, in addition to a list containing the minimum and maximum values the first gear ratio can bear.

import tutorials.tutorial9_simple_gearbox as objects
import numpy as np
import plot_data
from dessia_api_client import Client
 
"""
Engine efficiency map
"""
engine_speeds = list(np.linspace(500, 6000, num = 12)) #Engine speed in rpm
engine_speeds = [float(i)*np.pi/30 for i in engine_speeds]  # in rad/s
engine_torques = [15.6,31.2, 46.8, 62.4, 78, 93.6, 109.2, 124.8, 140.4, 156, 171.6] #engine torque in N*m
mass_flow_rate = [[0.1389, 0.2009, 0.2524, 0.3006, 0.3471, 0.4264, 0.4803, 0.5881, 0.5881, 0.6535, 0.7188],
                  [0.2777, 0.3659, 0.4582, 0.5587, 0.6453, 0.7792, 0.8977, 1.0325, 1.1762, 1.3069, 1.4376],
                  [0.4166, 0.5538, 0.7057, 0.8332, 0.9557, 1.0733, 1.2127, 1.3428, 1.5438, 1.9604, 2.1564],
                  [0.5391, 0.7188, 0.9116, 1.0913, 1.2497, 1.4115, 1.5552, 1.7774, 2.0290, 2.3851, 2.8752],
                  [0.6330, 0.8658, 1.0904, 1.2906, 1.5111, 1.6786, 1.9440, 2.2217, 2.4995, 2.8997, 3.5940],
                  [0.7106, 0.9949, 1.2718, 1.5193, 1.7888, 2.0878, 2.3671, 2.6661, 2.9993, 3.5286, 4.3128],
                  [0.7433, 1.0806, 1.3722, 1.7839, 2.2013, 2.5490, 2.8817, 3.1562, 3.5507, 4.1739, 5.0316],
                  [0.9475, 1.2938, 1.7290, 2.2087, 2.5648, 2.9993, 3.3391, 3.6855, 4.2932, 4.8355, 5.7504],
                  [1.1027, 1.6026, 2.1525, 2.5877, 2.9957, 3.4184, 3.8852, 4.4108, 5.0151, 5.6238, 6.4692],
                  [1.5519, 2.0910, 2.5730, 3.0222, 3.4715, 3.8717, 4.4998, 5.0642, 5.7781, 6.4528, 7.1880],
                  [1.8868, 2.5517, 3.1537, 3.6479, 4.0882, 4.4206, 5.2203, 5.8941, 6.5500, 7.2329, 7.9068],
                  [2.0584, 2.8817, 3.5286, 4.0775, 4.5578, 5.1165, 5.6948, 6.4300, 7.1455, 7.8414, 8.6256]] #mass flow rate in g/s
mass_flow_rate_kgps = []
for list_mass_flow_rate in mass_flow_rate:
    list_mass_flow = []
    for mass_flow in list_mass_flow_rate:
        list_mass_flow.append(mass_flow/1000)                                                                #mass flow rate in kg/s
    mass_flow_rate_kgps.append(list_mass_flow)
 
 
fuel_hv = 0.012068709                                                       # in kWh/g
fuel_hv = fuel_hv*3.6e9                                                    # in J/kg
efficiency_map = objects.EfficiencyMap(engine_speeds = engine_speeds, engine_torques = engine_torques, mass_flow_rate = mass_flow_rate_kgps, fuel_hv = fuel_hv)
 
 
"""
WLTP cycle
"""
 
cycle_speeds= [0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.2,3.1,5.7,8.0,10.1,12.0,13.8,15.4,16.7,17.7,18.3,18.8,
                18.9,18.4,16.9,14.3,10.8,7.1,4.0,0.0,0.0,0.0,0.0,1.5,3.8,5.6,7.5,9.2,10.8,12.4,13.8,15.2,16.3,17.3,18.0,
                18.8,19.5,20.2,20.9,21.7,22.4,23.1,23.7,24.4,25.1,25.4,25.2,23.4,21.8,19.7,17.3,14.7,12.0,9.4,5.6,3.1,0.0,
                0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,
                0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.7,1.1,1.9,2.5,3.5,4.7,6.1,7.5,9.4,11.0,12.9,14.5,
                16.4,18.0,20.0,21.5,23.5,25.0,26.8,28.2,30.0,31.4,32.5,33.2,33.4,33.7,33.9,34.2,34.4,34.7,34.9,35.2,35.4,
                35.7,35.9,36.6,37.5,38.4,39.3,40.0,40.6,41.1,41.4,41.6,41.8,41.8,41.9,41.9,42.0,42.0,42.2,42.3,42.6,43.0,
                43.3,43.7,44.0,44.3,44.5,44.6,44.6,44.5,44.4,44.3,44.2,44.1,44.0,43.9,43.8,43.7,43.6,43.5,43.4,43.3,43.1,
                42.9,42.7,42.5,42.3,42.2,42.2,42.2,42.3,42.4,42.5,42.7,42.9,43.1,43.2,43.3,43.4,43.4,43.2,42.9,42.6,42.2,
                41.9,41.5,41.0,40.5,39.9,39.3,38.7,38.1,37.5,36.9,36.3,35.7,35.1,34.5,33.9,33.6,33.5,33.6,33.9,34.3,34.7,
                35.1,35.5,35.9,36.4,36.9,37.4,37.9,38.3,38.7,39.1,39.3,39.5,39.7,39.9,40.0,40.1,40.2,40.3,40.4,40.5,40.5,
                40.4,40.3,40.2,40.1,39.7,38.8,37.4,35.6,33.4,31.2,29.1,27.6,26.6,26.2,26.3,26.7,27.5,28.4,29.4,30.4,31.2,
                31.9,32.5,33.0,33.4,33.8,34.1,34.3,34.3,33.9,33.3,32.6,31.8,30.7,29.6,28.6,27.8,27.0,26.4,25.8,25.3,24.9,
                24.5,24.2,24.0,23.8,23.6,23.5,23.4,23.3,23.3,23.2,23.1,23.0,22.8,22.5,22.1,21.7,21.1,20.4,19.5,18.5,17.6,
                16.6,15.7,14.9,14.3,14.1,14.0,13.9,13.8,13.7,13.6,13.5,13.4,13.3,13.2,13.2,13.2,13.4,13.5,13.7,13.8,14.0,
                14.1,14.3,14.4,14.4,14.4,14.3,14.3,14.0,13.0,11.4,10.2,8.0,7.0,6.0,5.5,5.0,4.5,4.0,3.5,3.0,2.5,2.0,1.5,
                1.0,0.5,0.0,0.0,0.0,0.0,0.0,0.0,2.2,4.5,6.6,8.6,10.6,12.5,14.4,16.3,17.9,19.1,19.9,20.3,20.5,20.7,21.0,
                21.6,22.6,23.7,24.8,25.7,26.2,26.4,26.4,26.4,26.5,26.6,26.8,26.9,27.2,27.5,28.0,28.8,29.9,31.0,31.9,32.5,
                32.6,32.4,32.0,31.3,30.3,28.0,27.0,24.0,22.5,19.0,17.5,14.0,12.5,9.0,7.5,4.0,2.9,0.0,0.0,0.0,0.0,0.0,0.0,
                0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,
                0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,
                0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.6,3.1,4.6,6.1,7.8,9.5,11.3,13.2,15.0,16.8,18.4,20.1,21.6,23.1,24.6,
                26.0,27.5,29.0,30.6,32.1,33.7,35.3,36.8,38.1,39.3,40.4,41.2,41.9,42.6,43.3,44.0,44.6,45.3,45.5,45.5,45.2,
                44.7,44.2,43.6,43.1,42.8,42.7,42.8,43.3,43.9,44.6,45.4,46.3,47.2,47.8,48.2,48.5,48.7,48.9,49.1,49.1,49.0,
                48.8,48.6,48.5,48.4,48.3,48.2,48.1,47.5,46.7,45.7,44.6,42.9,40.8,38.2,35.3,31.8,28.7,25.8,22.9,20.2,17.3,
                15.0,12.3,10.3,7.8,6.5,4.4,3.2,1.2,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,
                0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.6,1.9,2.7,5.2,7.0,9.6,11.4,14.1,15.8,
                18.2,19.7,21.8,23.2,24.7,25.8,26.7,27.2,27.7,28.1,28.4,28.7,29.0,29.2,29.4,29.4,29.3,28.9,28.5,28.1,27.6,
                26.9,26.0,24.6,22.8,21.0,19.5,18.6,18.4,19.0,20.1,21.5,23.1,24.9,26.4,27.9,29.2,30.4,31.6,32.8,34.0,35.1,
                36.3,37.4,38.6,39.6,40.6,41.6,42.4,43.0,43.6,44.0,44.4,44.8,45.2,45.6,46.0,46.5,47.0,47.5,48.0,48.6,49.1,
                49.7,50.2,50.8,51.3,51.8,52.3,52.9,53.4,54.0,54.5,55.1,55.6,56.2,56.7,57.3,57.9,58.4,58.8,58.9,58.4,58.1,
                57.6,56.9,56.3,55.7,55.3,55.0,54.7,54.5,54.4,54.3,54.2,54.1,53.8,53.5,53.0,52.6,52.2,51.9,51.7,51.7,51.8,
                52.0,52.3,52.6,52.9,53.1,53.2,53.3,53.3,53.4,53.5,53.7,54.0,54.4,54.9,55.6,56.3,57.1,57.9,58.8,59.6,60.3,
                60.9,61.3,61.7,61.8,61.8,61.6,61.2,60.8,60.4,59.9,59.4,58.9,58.6,58.2,57.9,57.7,57.5,57.2,57.0,56.8,56.6,
                56.6,56.7,57.1,57.6,58.2,59.0,59.8,60.6,61.4,62.2,62.9,63.5,64.2,64.4,64.4,64.0,63.5,62.9,62.4,62.0,61.6,
                61.4,61.2,61.0,60.7,60.2,59.6,58.9,58.1,57.2,56.3,55.3,54.4,53.4,52.4,51.4,50.4,49.4,48.5,47.5,46.5,45.4,
                44.3,43.1,42.0,40.8,39.7,38.8,38.1,37.4,37.1,36.9,37.0,37.5,37.8,38.2,38.6,39.1,39.6,40.1,40.7,41.3,41.9,
                42.7,43.4,44.2,45.0,45.9,46.8,47.7,48.7,49.7,50.6,51.6,52.5,53.3,54.1,54.7,55.3,55.7,56.1,56.4,56.7,57.1,
                57.5,58.0,58.7,59.3,60.0,60.6,61.3,61.5,61.5,61.4,61.2,60.5,60.0,59.5,58.9,58.4,57.9,57.5,57.1,56.7,56.4,
                56.1,55.8,55.5,55.3,55.0,54.7,54.4,54.2,54.0,53.9,53.7,53.6,53.5,53.4,53.3,53.2,53.1,53.0,53.0,53.0,53.0,
                53.0,53.0,52.8,52.5,51.9,51.1,50.2,49.2,48.2,47.3,46.4,45.6,45.0,44.3,43.8,43.3,42.8,42.4,42.0,41.6,41.1,
                40.3,39.5,38.6,37.7,36.7,36.2,36.0,36.2,37.0,38.0,39.0,39.7,40.2,40.7,41.2,41.7,42.2,42.7,43.2,43.6,44.0,
                44.2,44.4,44.5,44.6,44.7,44.6,44.5,44.4,44.2,44.1,43.7,43.3,42.8,42.3,41.6,40.7,39.8,38.8,37.8,36.9,36.1,
                35.5,35.0,34.7,34.4,34.1,33.9,33.6,33.3,33.0,32.7,32.3,31.9,31.5,31.0,30.6,30.2,29.7,29.1,28.4,27.6,26.8,
                26.0,25.1,24.2,23.3,22.4,21.5,20.6,19.7,18.8,17.7,16.4,14.9,13.2,11.3,9.4,7.5,5.6,3.7,1.9,1.0,0.0,0.0,0.0
                ,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,
                0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.2,3.1,5.7,8.0,10.1,12.0,13.8
                ,15.4,16.7,17.7,18.3,18.8,18.9,18.4,16.9,14.3,10.8,7.1,4.0,0.0,0.0,0.0,0.0,1.5,3.8,5.6,7.5,9.2,10.8,12.4,
                13.8,15.2,16.3,17.3,18.0,18.8,19.5,20.2,20.9,21.7,22.4,23.1,23.7,24.4,25.1,25.4,25.2,23.4,21.8,19.7,17.3,
                14.7,12.0,9.4,5.6,3.1,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,
                0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.7,1.1,1.9,2.5,3.5,4.7,
                6.1,7.5,9.4,11.0,12.9,14.5,16.4,18.0,20.0,21.5,23.5,25.0,26.8,28.2,30.0,31.4,32.5,33.2,33.4,33.7,33.9,
                34.2,34.4,34.7,34.9,35.2,35.4,35.7,35.9,36.6,37.5,38.4,39.3,40.0,40.6,41.1,41.4,41.6,41.8,41.8,41.9,41.9,
                42.0,42.0,42.2,42.3,42.6,43.0,43.3,43.7,44.0,44.3,44.5,44.6,44.6,44.5,44.4,44.3,44.2,44.1,44.0,43.9,43.8,
                43.7,43.6,43.5,43.4,43.3,43.1,42.9,42.7,42.5,42.3,42.2,42.2,42.2,42.3,42.4,42.5,42.7,42.9,43.1,43.2,43.3,
                43.4,43.4,43.2,42.9,42.6,42.2,41.9,41.5,41.0,40.5,39.9,39.3,38.7,38.1,37.5,36.9,36.3,35.7,35.1,34.5,33.9,
                33.6,33.5,33.6,33.9,34.3,34.7,35.1,35.5,35.9,36.4,36.9,37.4,37.9,38.3,38.7,39.1,39.3,39.5,39.7,39.9,40.0,
                40.1,40.2,40.3,40.4,40.5,40.5,40.4,40.3,40.2,40.1,39.7,38.8,37.4,35.6,33.4,31.2,29.1,27.6,26.6,26.2,26.3,
                26.7,27.5,28.4,29.4,30.4,31.2,31.9,32.5,33.0,33.4,33.8,34.1,34.3,34.3,33.9,33.3,32.6,31.8,30.7,29.6,28.6,
                27.8,27.0,26.4,25.8,25.3,24.9,24.5,24.2,24.0,23.8,23.6,23.5,23.4,23.3,23.3,23.2,23.1,23.0,22.8,22.5,22.1,
                21.7,21.1,20.4,19.5,18.5,17.6,16.6,15.7,14.9,14.3,14.1,14.0,13.9,13.8,13.7,13.6,13.5,13.4,13.3,13.2,13.2,
                13.2,13.4,13.5,13.7,13.8,14.0,14.1,14.3,14.4,14.4,14.4,14.3,14.3,14.0,13.0,11.4,10.2,8.0,7.0,6.0,5.5,5.0,
                4.5,4.0,3.5,3.0,2.5,2.0,1.5,1.0,0.5,0.0,0.0,0.0,0.0,0.0,0.0,2.2,4.5,6.6,8.6,10.6,12.5,14.4,16.3,17.9,19.1,
                19.9,20.3,20.5,20.7,21.0,21.6,22.6,23.7,24.8,25.7,26.2,26.4,26.4,26.4,26.5,26.6,26.8,26.9,27.2,27.5,28.0,
                28.8,29.9,31.0,31.9,32.5,32.6,32.4,32.0,31.3,30.3,28.0,27.0,24.0,22.5,19.0,17.5,14.0,12.5,9.0,7.5,4.0,
                2.9,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0
                ,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,
                0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,1.6,3.1,4.6,6.1,7.8,9.5,11.3,13.2,15.0,
                16.8,18.4,20.1,21.6,23.1,24.6,26.0,27.5,29.0,30.6,32.1,33.7,35.3,36.8,38.1,39.3,40.4,41.2,41.9,42.6,43.3,
                44.0,44.6,45.3,45.5,45.5,45.2,44.7,44.2,43.6,43.1,42.8,42.7,42.8,43.3,43.9,44.6,45.4,46.3,47.2,47.8,48.2,
                48.5,48.7,48.9,49.1,49.1,49.0,48.8,48.6,48.5,48.4,48.3,48.2,48.1,47.5,46.7,45.7,44.6,42.9,40.8,38.2,35.3,
                31.8,28.7,25.8,22.9,20.2,17.3,15.0,12.3,10.3,7.8,6.5,4.4,3.2,1.2,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,
                0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0]        # velocity in km/h
 
 
 
car_mass = 1524                                                             # Midsize car wheight in kilograms
dt = 1                                                                      # time interval in seconds
tire_radius = 0.1905                                                        # tire radius in m
cycle_speeds = [speed*1000/3600 for speed in cycle_speeds] #cycle speed in m/s
wltp_cycle = objects.WLTPCycle(cycle_speeds = cycle_speeds, car_mass = car_mass, tire_radius = tire_radius)
 
 
"""
Engine
"""
setpoint_speed = 600*np.pi/30 # in rad/s
setpoint_torque = 100
engine = objects.Engine(efficiency_map = efficiency_map, setpoint_speed = setpoint_speed, setpoint_torque = setpoint_torque)
 
"""
Gearbox
"""
speed_ranges = [[0, 30], [20 ,40], [30,50], [45, 70]] # in km/h
speed_ranges = [[speed_range[0]*(1000*2*np.pi)/(3600*np.pi*tire_radius), speed_range[1]*(1000*2*np.pi)/(3600*np.pi*tire_radius)] for speed_range in speed_ranges] #in rad/s
gearbox = objects.GearBox(engine = engine, speed_ranges = speed_ranges)
 
"""
GearBox Optimizer
"""
 
optimizer = objects.GearBoxOptimizer(gearbox = gearbox, wltp_cycle = wltp_cycle, first_gear_ratio_min_max = [.5, 4.5])
results = optimizer.optimize(1)

If you run the following code in the console, you will be able to see some plots that allow you to analyse what you get for one of the results

plot_data.plot_canvas(plot_data_object = results[0].plot_data()[0], canvas_id = 'canvas')
plot_data.plot_canvas(plot_data_object = results[0].plot_data()[1], canvas_id = 'canvas')

Here is one of the results you should get by running this code

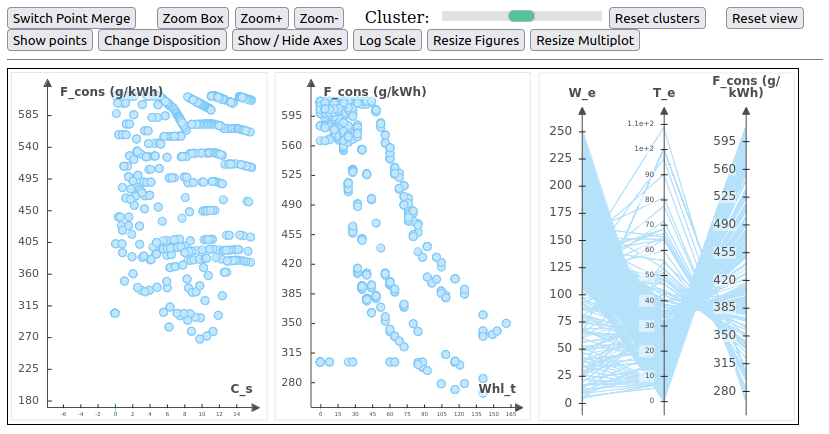
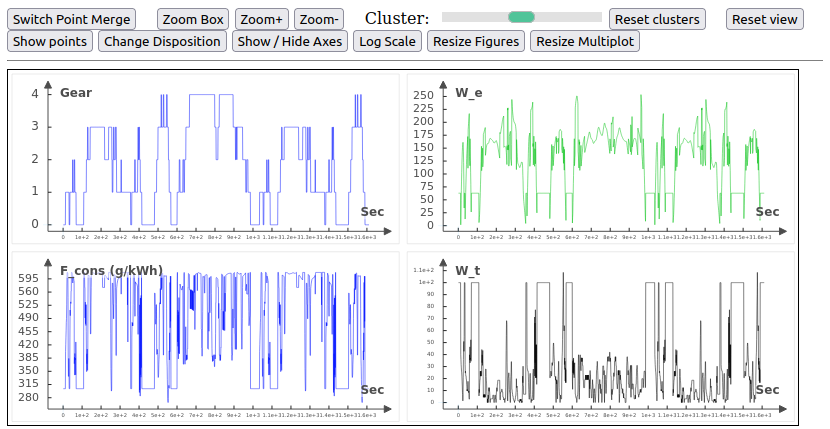
GBR plotdata 1 GBR plotdata 2

2.4 - Build a Workflow

Create a workflow for an optimizer

This part is about building a good workflow from the optimizer. The first step consists in transforming the Optimizer object into workflow blocks.

import tutorials.tutorial9_simple_gearbox as objects
import dessia_common.workflow as wf
import numpy as np
 
block_optimizer = wf.InstanciateModel(objects.GearBoxOptimizer, name='Gearbox Optimizer')
method_type = wf.MethodType(oclass_=bjects.GearBoxOptimizer, name='optimize')
method_optimize = wf.ModelMethod(method_type=method_type, name='Optimize')

Like the Optimizer, four other workflow blocks must be instantiated: an EfficiencyMap, a WLTPCycle, an Engine and a GearBox blocks

block_gearbox = wf.InstanciateModel(objects.GearBox, name='Gearbox')
block_engine = wf.InstanciateModel(objects.Engine, name= 'Engine')
 
block_efficiencymap = wf.InstanciateModel(objects.EfficiencyMap, name= 'Efficiency Map')
block_wltpcycle = wf.InstanciateModel(objects.WLTPCycle, name = 'WLTP Cycle')

Then, for the output results, a display workflow block is created, which receives a list of interesting attributes which will help compare all available solutions

list_attribute = ['average_fuel_consumption', 'average_engine_speed', 'average_engine_torque', 'ratio_min', 'ratio_max', 'average_ratio']
display = wf.MultiPlot(list_attribute, order = 1, name= 'Display')

To finish creating the workflow, the only step remaining is to connect the blocks

block_workflow = [block_optimizer, method_optimize, block_gearbox, block_engine, block_efficiencymap, block_wltpcycle, display]
pipe_workflow = [wf.Pipe(block_optimizer.outputs[0], method_optimize.inputs[0]),
                 wf.Pipe(block_gearbox.outputs[0], block_optimizer.inputs[0]),
                 wf.Pipe(block_wltpcycle.outputs[0], block_optimizer.inputs[1]),
                 wf.Pipe(block_engine.outputs[0], block_gearbox.inputs[0]),
                 wf.Pipe(block_efficiencymap.outputs[0], block_engine.inputs[0]),
                 wf.Pipe(method_optimize.outputs[0], display.inputs[0])]
 
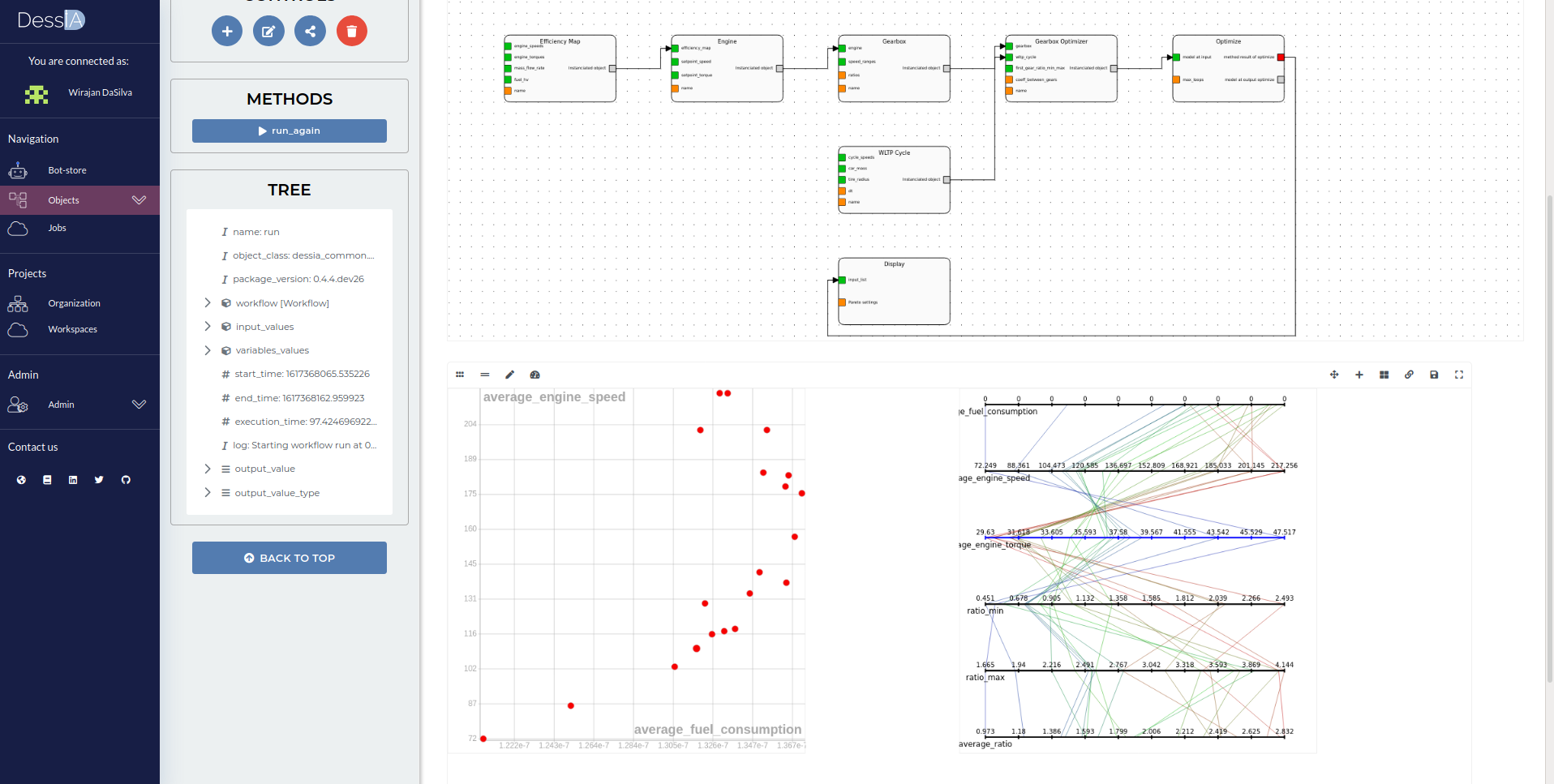
workflow = wf.Workflow(block_workflow, pipe_workflow, method_optimize.outputs[0])

Running the code and plotting the workflow using "workflow.plot_jointjs()" should display the following result:

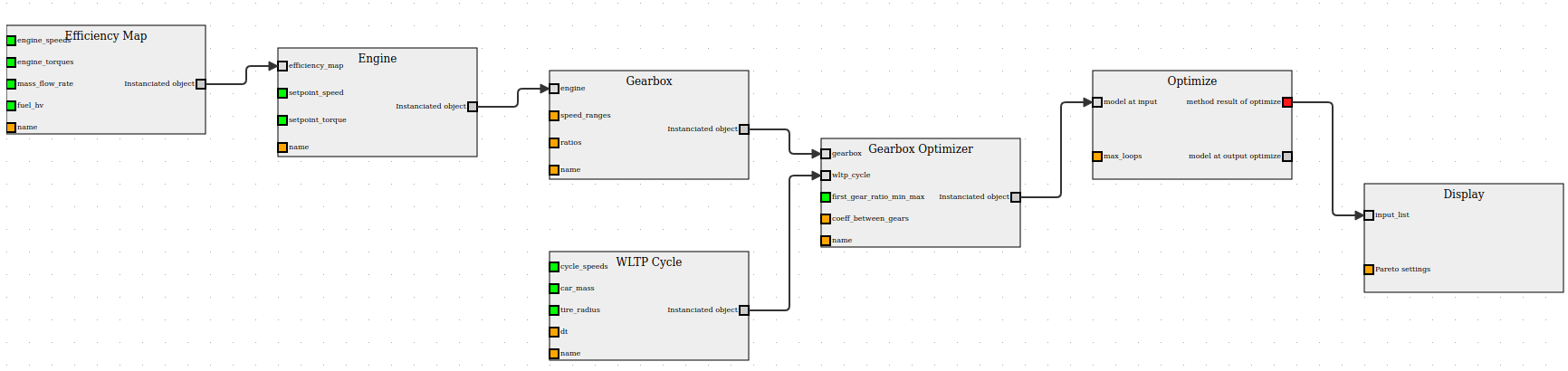
tutorial-9-workflow

While specifying the input values of the workflow, the block_optimizer has one input(firstgear_ratio_min_max), the _method_optimize has one input(maxloops) the _block_gearbox has one input (speedranges), the _block_engine has two inputs (1:setpointspeed, 2:setpoint_torque), the _block_efficiencymap has 4 inputs (1: enginespeeds, 2: enigne_torques, 3: f mass_fuel_rate, 4: Q_hv) and finally the _block_wltpcycle has three inputs (1: cycle_speeds, 2:car_mass, 3: tire_radius)

input_values = {workflow.index(block_optimizer.inputs[2]): [.5, 4.5],
                workflow.index(method_optimize.inputs[1]): 5,
                workflow.index(block_gearbox.inputs[1]):speed_ranges,
                workflow.index(block_engine.inputs[1]):setpoint_speed,
                workflow.index(block_engine.inputs[2]):setpoint_torque,
                workflow.index(block_efficiencymap.inputs[0]):engine_speeds,
                workflow.index(block_efficiencymap.inputs[1]):engine_torques,
                workflow.index(block_efficiencymap.inputs[2]):mass_flow_rate_kgps,
                workflow.index(block_efficiencymap.inputs[3]):fuel_hv,
                workflow.index(block_wltpcycle.inputs[0]):cycle_speeds,
                workflow.index(block_wltpcycle.inputs[1]):car_mass,
                workflow.index(block_wltpcycle.inputs[2]):tire_radius}
 
workflow_run = workflow.run(input_values)

As a result for the workflow_run you should get a list GearBoxResults. If you are able to connect to the DessIA platform, you can also import the workflow_run and visualize the plots on the platform and have the all the advantages it gives you to manipulate your results.

from dessia_api_client import Client
 
workflow_run = workflow.run(input_values)
 
c = Client(api_url = 'https://api.demo.dessia.tech')
r = c.create_object_from_python_object(workflow_run)

This is what you get if you use the platform

workflow-platform

Piping in constraint environment Simple Gearbox Generation